GiggleLiu - The Numeric Monster

Solving random walk on graphs with tails

References

  1. Quantum scattering theory on graphs with tails (Martin Varbanov, Todd A. Brun, 2009)

Half chain

Let the hamiltonian of a half chain be

H1/2=12∑n=0∞∣n⟩⟨n+1∣+h.c.H_{1/2} = \frac{1}{2} \sum_{n=0}^\infty |n\rangle\langle {n+1}| + h.c.

The eigenvalues and eigenvectors of a full chain are cos⁡(k)\cos(k) and ∣k⟩=eikn∣n⟩| k\rangle = e^{ikn} |n\rangle respectively. Given an eigenvector of a full chain, the effect of applying the half chain Hamiltonian on it is

H1/2∣k⟩1/2=∑n=0∞12eikn(∣n−1⟩+∣n+1⟩)=∑n=0∞(12(eik(n−1)+eik(n+1))∣n⟩)−12e−ik∣0⟩=cos⁡(k)∣k⟩1/2−12e−ik∣0⟩ \begin{align*} H_{1/2} |k\rangle_{1/2} &= \sum_{n=0}^{\infty}\frac{1}{2}e^{ikn}(|n-1\rangle + |n+1\rangle)\\ &= \sum_{n=0}^{\infty}\left(\frac{1}{2}(e^{ik(n-1)}+e^{ik(n+1)})|n\rangle\right) - \frac{1}{2}e^{-ik}|0\rangle\\ &=\cos(k) |k\rangle_{1/2} - \frac{1}{2}e^{-ik}|0\rangle \end{align*}

where ∣k⟩1/2=∑n=0∞∣n⟩⟨n∣k⟩|k\rangle_{1/2} = \sum_{n=0}^{\infty} |n\rangle\langle n|k\rangle.

Graphs with tails

Let G=(V,E)G=(V,E) be a graph with some of its vertices V′⊆VV'\subseteq V attached to half chains (or tails) and each vertex can be attached to at most one tail. The model Hamiltonian is

H=HG+∑v∈V′Hv H = H_G + \sum_{v\in V'} H_v

where Hv=12∑n=0∞∣nv⟩⟨n+1v∣+h.c.H_v = \frac{1}{2} \sum_{n=0}^\infty |n_v\rangle\langle {n+1}_v| + h.c. is a 1D chain model and HGH_G is the Hamiltonian on a graph. In the following, unless specified explicitly, ∑v\sum_v stands for ∑v∈V′\sum_{v\in V'}. Let us decompose the wave function on the graph into three parts.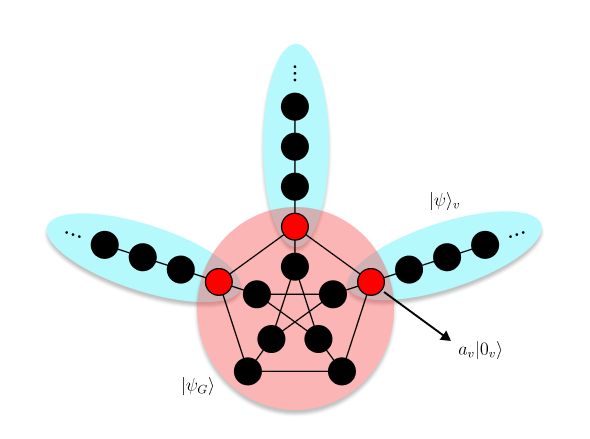

∣ψ⟩=∣ψ⟩G+∑v∣ψ⟩v−∑vav∣0v⟩ \begin{equation*} |\psi\rangle = |\psi\rangle_G + \sum_v |\psi\rangle_v - \sum_v a_v|0_v\rangle \end{equation*}

where ∣ψ⟩G=∑v∈V∣v⟩⟨v∣ψ⟩|\psi\rangle_G = \sum_{v\in V}|v\rangle\langle v|\psi\rangle (note in our definition, ∣v⟩=∣0v⟩|v\rangle = |0_v\rangle), ∣ψ⟩v=∑n=0∞∣nv⟩⟨nv∣ψ⟩|\psi\rangle_v = \sum_{n=0}^\infty|n_v\rangle\langle n_v|\psi\rangle and av=⟨0v∣ψ⟩G=⟨0v∣ψ⟩va_v = \langle 0_v|\psi\rangle_G = \langle 0_v|\psi\rangle_v.

To solve the eigen-decomposition problem H∣ψ⟩=E∣ψ⟩H |\psi\rangle = E|\psi\rangle, we have

H∣ψ⟩=HG∣ψ⟩G+HG∑v(∣ψ⟩v−av∣0v⟩)+∑vHv(∣ψ⟩G−∑v′av′∣0v′⟩)+∑vHv∣ψ⟩v \begin{align*} H |\psi\rangle &= H_G |\psi\rangle_G \textcolor{lightgray}{+ H_G\sum_v(|\psi\rangle_v - a_v|0_v\rangle)}\\ &\textcolor{lightgray}{+\sum_v H_v (|\psi\rangle_G - \sum_{v'} a_{v'}|0_{v'}\rangle)} + \sum_v H_v|\psi\rangle_v \end{align*}

where gray parts are zeroed out.

Propagating states

Let us assume ∣ψ⟩v=Iv∣−k⟩+Rv∣k⟩|\psi\rangle_v = I_v|-k\rangle + R_v|k\rangle, we have

av=Iv+Rv.a_v = I_v+R_v.

By inserting (2) to (5), we have

H∣ψ⟩=HG∣ψ⟩G+∑vcos⁡(k)∣ψ⟩v−(Iv2eik+Rv2e−ik)∣0v⟩ H |\psi\rangle = H_G |\psi\rangle_G + \sum_v \cos(k)|\psi\rangle_v - \left(\frac{I_v}{2}e^{ik} + \frac{R_v}{2}e^{-ik}\right)|0_v\rangle

For this ansatz, the eigenvalue of HH has to be E=cos⁡(k)E=\cos(k). By using (4) and (6)

cos⁡(k)(∣ψ⟩G+∑v∣ψ⟩v−∑v(Iv+Rv)∣0v⟩)=HG∣ψ⟩G+∑vcos⁡(k)∣ψ⟩v−∑v(Iv2eik+Rv2e−ik)∣0v⟩ \begin{align*} &\cos(k) \left(|\psi\rangle_G \textcolor{lightgray}{+ \sum_v |\psi\rangle_v} - \sum_v (I_v + R_v)|0_v\rangle\right) \\ = &H_G |\psi\rangle_G \textcolor{lightgray}{+ \sum_v \cos(k)|\psi\rangle_v} - \sum_v\left(\frac{I_v}{2}e^{ik} + \frac{R_v}{2}e^{-ik}\right)|0_v\rangle \end{align*}

That is

HG∣ψ⟩G=cos⁡(k)∣ψ⟩G+∑v(−cos⁡(k)(Iv+Rv)+Iv2eik+Rv2e−ik)∣0v⟩=cos⁡(k)∣ψ⟩G−∑v(Iv2e−ik+Rv2eik)∣0v⟩ \begin{align*} H_G|\psi\rangle_G = &\cos(k) |\psi\rangle_G+ \sum_{v}\left(-\cos(k)(I_v + R_v) +\frac{I_v}{2}e^{ik} + \frac{R_v}{2}e^{-ik}\right)|0_v\rangle\\ = &\cos(k) |\psi\rangle_G- \sum_{v}\left(\frac{I_v}{2}e^{-ik} + \frac{R_v}{2}e^{ik}\right)|0_v\rangle \end{align*}

Let us assume the scattering is from vertex ww, i.e. Iw=1I_w = 1 and Iv≠w=0I_{v\neq w} = 0. We have

HG∣ψ⟩G=cos⁡(k)∣ψ⟩G−12e−ik∣0w⟩−∑vRv2eik∣0v⟩ \begin{align*} H_G|\psi\rangle_G = &\cos(k) |\psi\rangle_G-\frac{1}{2}e^{-ik}|0_w\rangle - \sum_{v}\frac{R_v}{2}e^{ik}|0_v\rangle \end{align*}

Key point: Equation (11) is a quadratic linear equation

Let z=eikz = e^{ik}, we have

2HGz∣ψ⟩G=(1+z2)∣ψ⟩G−∣0w⟩−∑vRvz2∣0v⟩(1−2HGz+Qz2)∣ψ⟩G=(1−z2)∣0w⟩ \begin{align*} &2H_G z|\psi\rangle_G = (1+z^2) |\psi\rangle_G-|0_w\rangle - \sum_{v}R_vz^2|0_v\rangle\\ &(1 - 2H_G z + Q z^2)|\psi\rangle_G = (1-z^2)|0_w\rangle \end{align*}

where

Q=1−∑v∣0v⟩⟨0v∣ Q = 1 - \sum_v| 0_v\rangle\langle 0_v |

since

av=⟨0v∣ψ⟩G={Rv,v≠w1+Rw,v=w a_v = \langle 0_v|\psi\rangle_G = \begin{cases} R_v &, v \neq w\\ 1+R_w &, v = w \end{cases}

Except the −2-2 before HGH_G due to the difference in convension, (11) is the same as Eq. 12 in Ref. 1.

Bound states

There are two types of bound states. The first type with ∣ψ⟩v=0|\psi\rangle_v = 0 is trivial. In the following, we discuss the second type: k=iκk = i\kappa is pure imaginary. Let us assume

∣ψ⟩v=av∣κ⟩|\psi\rangle_v = a_v|\kappa\rangle

with ∣κ⟩=e−κnv∣nv⟩|\kappa\rangle = e^{-\kappa n_v} |n_v\rangle. Following the same derivation from (7) to (11), we have

H∣ψ⟩=HG∣ψ⟩G+∑vcosh⁡(κ)∣ψ⟩v−av2eκ∣0v⟩ H |\psi\rangle = H_G |\psi\rangle_G + \sum_v \cosh(\kappa)|\psi\rangle_v - \frac{a_v}{2}e^{\kappa}|0_v\rangle

For this ansatz, the eigenvalue of HH has to be E=cosh⁡(κ)E=\cosh(\kappa). By using (4) and (14)

cosh⁡(κ)(∣ψ⟩G+∑v∣ψ⟩v−∑vav∣0v⟩)=HG∣ψ⟩G+∑vcosh⁡(κ)∣ψ⟩v−∑vav2eκ∣0v⟩,HG∣ψ⟩G=cosh⁡(κ)∣ψ⟩G−∑vav2e−κ∣0v⟩ \begin{align*} &\cosh(\kappa) \left(|\psi\rangle_G \textcolor{lightgray}{+ \sum_v |\psi\rangle_v} - \sum_v a_v|0_v\rangle\right) \\ = &H_G |\psi\rangle_G \textcolor{lightgray}{+ \sum_v \cosh(\kappa)|\psi\rangle_v} - \sum_v\frac{a_v}{2}e^{\kappa}|0_v\rangle,\\ &H_G|\psi\rangle_G = \cosh(\kappa) |\psi\rangle_G - \sum_{v}\frac{a_v}{2}e^{-\kappa}|0_v\rangle\\ \end{align*}

Let zb=e−κz_b = e^{-\kappa}, we have a new quadratic linear equation for the bounded states

(1−2HGzb+Qzb2)∣ψ⟩G=0 (1-2H_Gz_b+Qz_b^2)|\psi\rangle_G = 0
CC BY-SA 4.0 GiggleLiu. Last modified: April 04, 2024. Website built with Franklin.jl and the Julia programming language.