GiggleLiu - The Numeric Monster

The landscape of a quantum circuit

This section is a simplified discussion of results in Ref. 5.

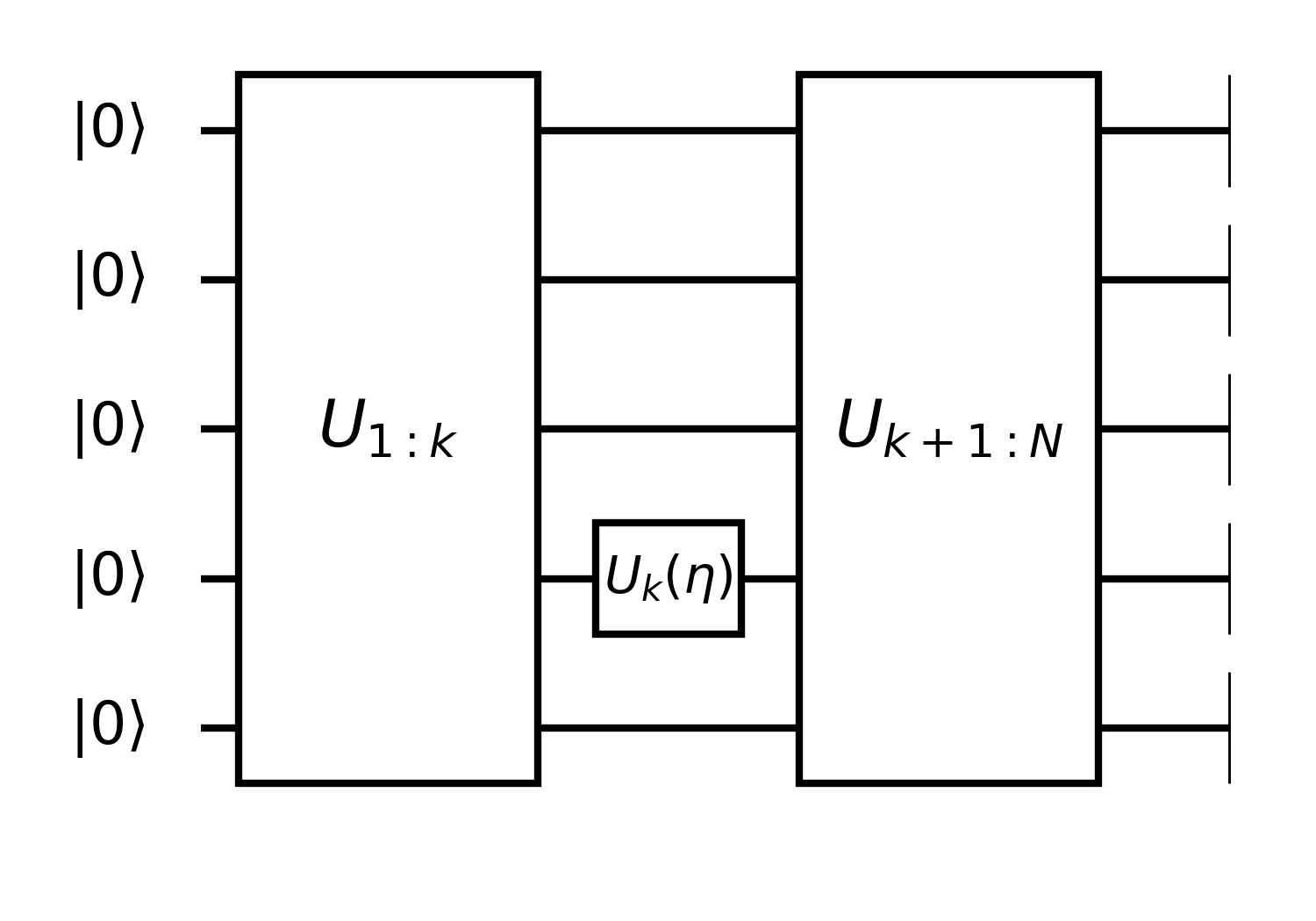
Consider the expectation value of BB on state ∣ψN⟩=UN:k+1Uk(η)Uk−1:1∣ψ0⟩\vert\psi_N\rangle = U_{N:k+1} U_k(\eta)U_{k-1:1}\vert\psi_0\rangle with Uk(η)=e−iΞη/2U_k(\eta)=e^{-i\Xi\eta/2}. Given Ξ2=1\Xi^2 =1, we have Uk(η)=cos⁡(η2)−isin⁡(η2)ΞU_k(\eta) = \cos(\frac{\eta}{2})-i\sin(\frac{\eta}{2})\Xi.

⟨B⟩=⟨ψk∣[cos⁡η2+isin⁡η2Ξ]B~k+1[cos⁡η2−isin⁡η2Ξ]∣ψk⟩=cos⁡2η2⟨ψk∣B~k+1∣ψk⟩+sin⁡2η2⟨ψk∣ΞB~k+1Ξ∣ψk⟩+isin⁡η2cos⁡η2⟨ψk∣[Ξ,B~k+1]∣ψk⟩=cos⁡2η2(⟨ψk∣B~k+1−ΞB~k+1Ξ∣ψk⟩)+isin⁡η2⟨ψk∣[Ξ,B~k+1]∣ψk⟩+⟨ψk∣ΞB~k+1Ξ∣ψk⟩=cos⁡η2(⟨ψk∣B~k+1−ΞB~k+1Ξ∣ψk⟩)+isin⁡η2⟨ψk∣[Ξ,B~k+1]∣ψk⟩+12⟨ψk∣B~+ΞB~k+1Ξ∣ψk⟩=αcos⁡η+βsin⁡η+γ=rcos⁡(η−ϕ)+γ \begin{align*} \langle B\rangle &= \langle \psi_k| \left[\cos\frac{\eta}{2}+i\sin\frac{\eta}{2}\Xi\right] \tilde{B}_{k+1} \left[\cos\frac{\eta}{2}-i\sin\frac{\eta}{2}\Xi\right]|\psi_k\rangle\\ &= \cos^2\frac{\eta}{2}\langle\psi_k| \tilde{B}_{k+1}|\psi_k\rangle +\sin^2\frac{\eta}{2}\langle\psi_k|\Xi \tilde{B}_{k+1}\Xi|\psi_k\rangle + i\sin\frac{\eta}{2}\cos\frac{\eta}{2}\langle\psi_k|\left[\Xi, \tilde{B}_{k+1}\right]|\psi_k\rangle\\ &=\cos^2\frac{\eta}{2}\left(\langle\psi_k|\tilde{B}_{k+1}-\Xi \tilde{B}_{k+1}\Xi|\psi_k\rangle\right)+ i\frac{\sin\eta}{2}\langle\psi_k|\left[\Xi, \tilde{B}_{k+1}\right]|\psi_k\rangle + \langle\psi_k|\Xi \tilde{B}_{k+1}\Xi|\psi_k\rangle\\ &=\frac{\cos\eta}{2}\left(\langle\psi_k|\tilde{B}_{k+1}-\Xi \tilde{B}_{k+1}\Xi|\psi_k\rangle\right)+ i\frac{\sin\eta}{2}\langle\psi_k|\left[\Xi, \tilde{B}_{k+1}\right]|\psi_k\rangle + \frac{1}{2}\langle\psi_k|\tilde{B}+\Xi \tilde{B}_{k+1}\Xi|\psi_k\rangle\\ &=\alpha\cos\eta+ \beta\sin\eta+\gamma\\ & = r\cos(\eta-\phi)+\gamma \end{align*}

Here, In line 1, we used the following shorthands

∣ψk⟩=Uk:1∣ψ0⟩B~k+1=UN:k+1†BUN:k+1 \begin{align*} &|\psi_{k}\rangle = U_{k:1}|\psi_0\rangle\\ &\tilde{B}_{k+1} = U_{N:k+1}^\dagger B U_{N:k+1} \end{align*}

And in line 5, we have introduced

α=12(⟨ψk∣B~k+1−ΞB~k+1Ξ∣ψk⟩),β=i12⟨ψk∣[Ξ,B~k+1]∣ψk⟩,γ=12⟨ψk∣B~+ΞB~k+1Ξ∣ψk⟩. \begin{align*} \alpha &= \frac{1}{2}\left(\langle\psi_k\vert\tilde{B}{k+1}-\Xi \tilde{B}{k+1}\Xi\vert\psi_k\rangle\right),\\ \beta &= i\frac{1}{2}\langle\psi_k\vert\left[\Xi, \tilde{B}{k+1}\right]\vert\psi_k\rangle,\\ \gamma &= \frac{1}{2}\langle\psi_k\vert\tilde{B}+\Xi \tilde{B}{k+1}\Xi\vert\psi_k\rangle. \end{align*}

Finally, we obtained a sine function.

A direct proposition is

∂⟨B⟩η∂η=12(⟨B⟩η+π2−⟨B⟩η−π2) \frac{\partial \langle B\rangle_\eta}{\partial \eta} = \frac{1}{2}(\langle B\rangle_{\eta+\frac{\pi}{2}} - \langle B\rangle_{\eta-\frac{\pi}{2}})

For statistic functional

Next, we describe a new class of differenciable loss which can not be written as an obserable easily, the statistic functionals, for simplicity, we consider an arbitrary statistic functional f(X)f(\mathbf{X}), with a sequence of bit strings X≡{x1,x2,…,xr}\mathbf{X}\equiv\{x_1,x_2,\ldots, x_r\} as its arguments. Let's define the following expectation of this function

Ef(Γ)≡E{xi∼pθ+γi}i=1r[f(X)].\mathbb{E}_f(\boldsymbol{\Gamma})\equiv\mathop{\mathbb{E}}\limits_{\substack{\{x_i\sim p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_i}\}_{i=1}^{r}}}\left[f(\mathbf{X})\right].

Here, Γ={γ1,γ2,…,γr}\boldsymbol{\Gamma}=\{\boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2,\ldots,\boldsymbol{\gamma}_r\} is the offset angles applied to circuit parameters, %Its element γi\boldsymbol{\gamma}_i is defined in the same parameter space as θ\boldsymbol{\theta} that represents a shift to θ\boldsymbol{\theta}. which means the probability distributions of generated samples is {pθ+γ1,pθ+γ2,…,pθ+γr}\{p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_1}, p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_2},\ldots ,p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_r}\}. Writing out the above expectation explicitly, we have

Ef(Γ)=∑Xf(X)∏ipθ+γi(xi),\mathbb{E}_f(\boldsymbol{\Gamma})=\sum\limits_\mathbf{X} f(\mathbf{X})\prod\limits_i p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_i}(x_i),

where index ii runs from 11 to rr. Its partial derivative with respect to θlα\theta^\alpha_l is

∂Ef(Γ)∂θlα=∑Xf(X)∑j∂pθ+γj(xj)∂θlα∏i≠jpθ+γi(xi)\frac{\partial \mathbb{E}_f(\boldsymbol{\Gamma})}{\partial \theta^\alpha_l}=\sum\limits_\mathbf{X} f(\mathbf{X})\sum\limits_j\frac{\partial p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_j}(x_j)}{\partial\theta^\alpha_l}\prod\limits_{i\neq j} p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_i}(x_i)

Again, using the gradient of probability, we have

∂Ef(Γ)∂θlα=12∑j,s=±∑Xf(X)pθ+γj+sπ2elα(xj)∏i≠jpθ+γi(xi)=12∑j,s=±Ef({γi+sδijπ2elα}i=1r) \begin{align*} \frac{\partial \mathbb{E}_f(\boldsymbol{\Gamma})}{\partial \theta^\alpha_l}&=\frac{1}{2}\sum\limits_{j,s=\pm}\sum\limits_\mathbf{X} f(\mathbf{X}){p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_j+s\frac{\pi}{2}\mathbf{e}_l^\alpha}(x_j)}\prod\limits_{i\neq j} p_{\boldsymbol{\theta}+\boldsymbol{\gamma}_i}(x_i)\\ &=\frac{1}{2}\sum\limits_{j,s=\pm}\mathbb{E}_f(\{\boldsymbol{\gamma}_i+s\delta_{ij}\frac{\pi}{2}\mathbf{e}_l^\alpha\}_{i=1}^{r})\end {align*}

If ff is symmetric, Ef(0)\mathbb{E}_f(\mathbf{0}) becomes a V-statistic [Mises (1947)], then the gradient can be further simplified to

∂Ef(Γ)∂θlα=r2∑s=±Ef({γ0+sπ2elα,γ1,…,γr}), \begin{align} \frac{\partial \mathbb{E}_f(\boldsymbol{\Gamma})}{\partial \theta^\alpha_l}=\frac{r}{2}\sum\limits_{s=\pm}\mathbb{E}_f\left(\{\boldsymbol{\gamma}_0+s\frac{\pi}{2}\mathbf{e}_l^\alpha,\boldsymbol{\gamma}_1,\ldots,\boldsymbol{\gamma}_r\}\right), \end{align}

which contains only two terms. This result can be readily verified by calculating the gradient of MMD loss, noticing the expectation of a kernel function is a V-statistic of degree 22. By repeatedly applying the gradient formula, we will be able to obtain higher order gradients.

References

  1. Jin-Guo Liu and Lei Wang, arXiv:1804.04168

  2. J. Li, X. Yang, X. Peng, and C.-P. Sun, Phys. Rev. Lett. 118,

150503 (2017).

  1. E. Farhi and H. Neven, arXiv:1802.06002.

  2. K. Mitarai, M. Negoro, M. Kitagawa, and K. Fujii,

arXiv:1803.00745.

  1. Nakanishi, Ken M., Keisuke Fujii, and Synge Todo.

arXiv:1903.12166 (2019).

CC BY-SA 4.0 GiggleLiu. Last modified: April 04, 2024. Website built with Franklin.jl and the Julia programming language.