Understanding our computing devices (draft)
Understanding our computing devices (draft)
Scientific computing is a combination of scientific applications, mathematical modeling and high performance computing. The first lecture focuses on understanding our computing devices and understand how to get high performance from them.
Computer architechture
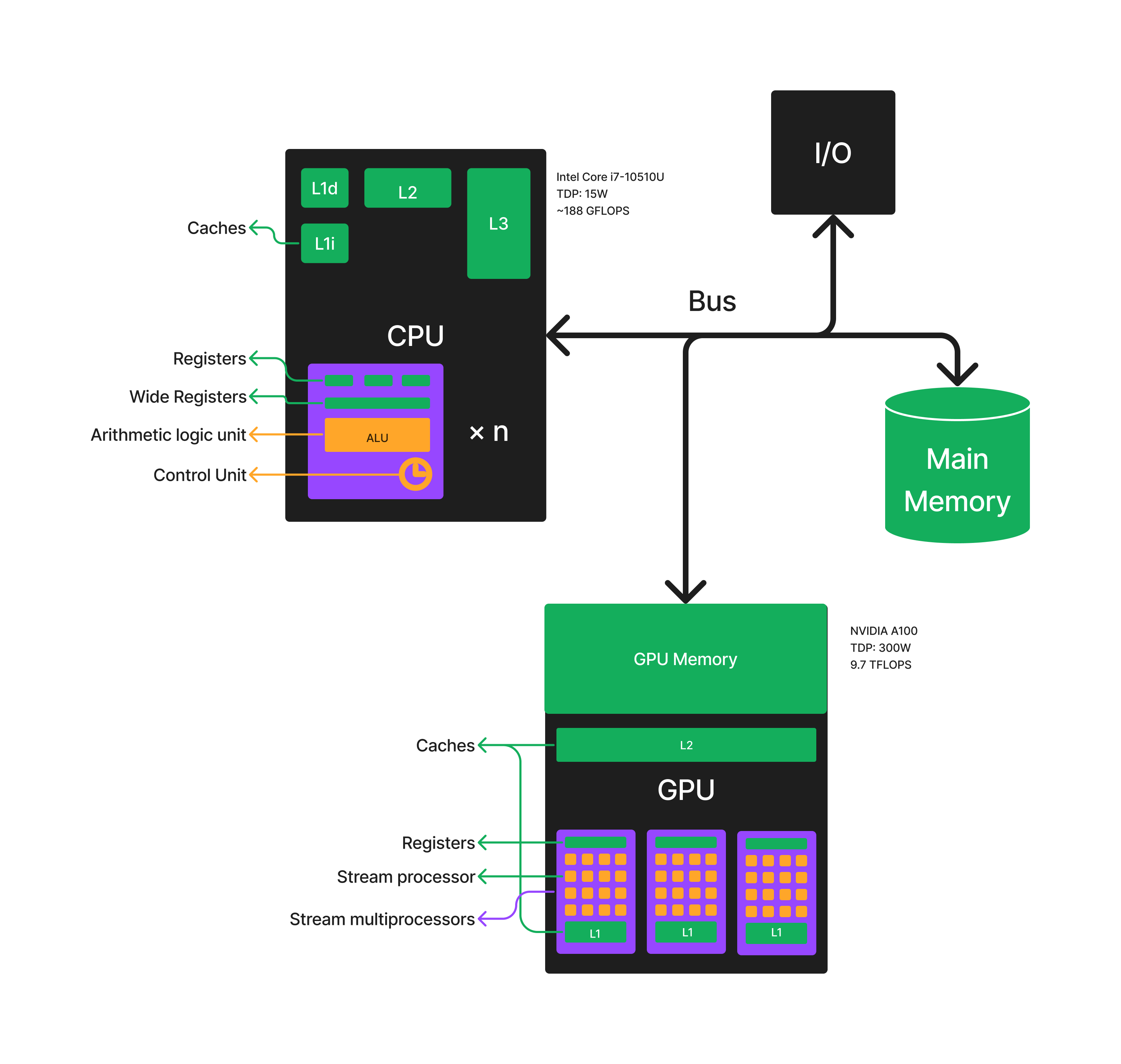
The Von Neumann architecture design consists of a Control Unit, Arithmetic and Logic Unit (ALU), Memory Unit, Registers and Inputs/Outputs, while the control unit, ALU, and registers are all contained in a central processing unit (CPU).
As illustrated above (click the image to make it larger), a modern computer contains the following building blocks
A CPU
A CPU clock signal is originally generated by quartz crystal oscillators of about 20MHz or so, and then the frequency is multiplied by one or more phase-locked loops to generate the clock signals for different parts of the system. (such as 4GHz for a CPU core).
A control unit is circuitry within a computer’s processor that directs operations. It instructs the memory, logic unit, and both output and input devices of the computer on how to respond to the program’s instructions. CPUs and GPUs are examples of devices that use control units.
Registers are the fastest "storage" shiped with CPU, directly accessible to the processor and works in the same clock rate as the CPU clock. The size of a general purposed register in a x64 machine is typically 64 bit while some wide registers designed for Single Instruction, Multiple Data (SIMD) can be several times larger, which allows processing multiple data points simultaneously with a single instruction. For example, if your computer supports the
avx2instruction set, there must be a wide register of size 256 (four 64-bit floating point numbers).An ALU is a combinational digital circuit that performs arithmetic and bitwise operations on integer binary numbers.
The memory hierarchy separates computer storage into a hierarchy based on response time. The fastest-smallest L1 cache works in the same speed as CPU, while the slowest-largest main memory has a ~50ns latency.
A system bus is a single computer bus that connects the major components of a computer system, combining the functions of a data bus to carry information, an address bus to determine where it should be sent or read from, and a control bus to determine its operation.
I/O devices are the pieces of hardware used by a human (or other system) to communicate with a computer. For instance, a keyboard or computer mouse is an input device for a computer, while monitors and printers are output devices.
For some devices, it also contains
General-purpose computing on graphics processing units (GPGPU) is the use of a graphics processing unit (GPU), which typically handles computation only for computer graphics, to perform computation in applications traditionally handled by the central processing unit (CPU). The CUDA architecture is built around a scalable array of multithreaded Streaming Multiprocessors (SMs).
Compiling process
A program is compiled to binaries (e.g. 010011...) in the main memory of a computer. The binary encodes both instructions and data, while a instruction can be an arithematic/logical operation to manipulate data in registers, transfering data from the main memory to registers and vise versa, or branching. For different computing devices, the supported instruction sets can be very different.
To execute the binary, the computing device (e.g. a CPU or a GPU) first loads the instructions from the memory to the instruction register. After performing the arithmetic/logical instructions on the data in registers, the data in the result register is copied back to the main memory.
In practise, a user program is executed in an operating system, which is a special software that manages the computing resources for other programs. It devides the computing time into small chunks of size ranging from milliseconds to tens of milliseconds and allocate them to different processes.
Memory bandwidth and latency
Memory bandwidth is the speed of data transmission speed from the main memory to the registers, which is much slower than the speed of computing devices manipulating the data. To get the designed peak performance from your computing devices, you need to perform a certain number of operations on a data before deallocating it from the cache. The expected arithmetic indensity is defined as the ratio between the FLOPS and data rate, which is equal to the number of operations to be done on a data to equate the time spent on data transmission and manipulation. You may find a good introduction about the latency problem in this youtube clip.
The following is a table from the above video,
| Intel Xeon 8280 | NVIDIA A100 | |
|---|---|---|
| Clock Cycle | 0.37ns | 0.71ns |
| Peak FP32 GFLOPS | 2190 | 19500 |
| Memory bandwidth (GB/s) | 131 | 1555 |
| DRAM Latency (ns) | 89 | 404 |
Peak FP32 GFLOPS means the maximum number of single precision (32 bit) floating point operations per second, which is a standard measure of device performance. THe memory bandwidth is computed in unit of Giga-Byte per second, where 1 byte = 8 bits. DRAM is the dynamic random access memory, serving as the main memory.
We can read from this table that typically
a GPU works in a much lower clock speed that a CPU.
a GPU has much larger computing power in the terms of FLOPS, because it has many CUDA cores (stream processors).
the bandwidth of a GPU is much larger than that of a CPU. Comparing with their computing power, the bandwidth is small in both cases. Only if the data in the cache can be reused for certain number of times, i.e. high arithematic intensity, the computing power of a device can be the actual bottleneck.
The latency is several orders larger than the CPU/GPU clock time, which physically bottlenecked by the speed of light.
One of the main differences between CPU and GPU architectures are due to their different approaches to solve the latency issue. CPUs are highly optimized for reducing the latency, i.e. to solve a task as soon as possible. Engineers designed a complicated 3-level caching system for CPUs that exists in the majority of our modern computers. Caches belongs to the static random access memory (SRAM), which is much faster to access than the main memory or the dynamic random access memory (DRAM) we talk about in our daily life. As is illustrated in the figure, by the order of decreasing speed and increasing size, caches include fastest L1 cache working in the same speed as CPU, slower L2 cache, and the slowest L3 cache but still faster than the DRAM. When loading data from the main memory to a register, the CPU looks up the L1 cache first. If the CPU cannot find the data it is looking for in the L1 cache (or cache miss), it checks the L2 cache and L3 cache in order. Once the desired data is found in the main memory, not only the required data, but also its physical neighbors are loaded to the caches. The wisdom behind the caching system is data locality, i.e. whenever a data is used, the data physically close to it has much higher probability to be used than the rest. Locality is particularly true when a program perform elementwise operations to an array with contiguous storage.
When loading a 32/64-bit data from the memory to a register, the computer loads a chunk of data to the caches. The wisdom behind this design is the locallity of data using, i.e. a data is much more likely to be used if it is physically close to the data currently in use.
GPUs hide the latency issues by launching a lot of threads at the same time. When one thread gets stuck and waiting, a GPU simply trys to find another thread that is about to execute. Without enough threads, a GPU will be latency bottlenecked. In Compute Unified Device Architecture (CUDA) programming, the number of CUDA cores determines the number of threads that can be simultaneously executed. CUDA cores are very similar to CPU cores, while the number of which can easily go up to several thousand, they are not as independent as CPU cores. The style of the execution of CUDA programs are called single instruction multiple threads (SIMT), in which multiple data can be processed by a single instruction. While the style how CPU cores work is called multiple instruction multiple data (MIMD), which does not require all threads to execute the same instruction.
Hands on: Get CPU and memory information
The computing power of a CPU
In the linux system, the CPU information can be printed by typing lscpu.
$ lscpu
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Address sizes: 39 bits physical, 48 bits virtual
Byte Order: Little Endian
CPU(s): 8
On-line CPU(s) list: 0-7
Vendor ID: GenuineIntel
Model name: Intel(R) Core(TM) i7-10510U CPU @ 1.80GHz
CPU family: 6
Model: 142
Thread(s) per core: 2
Core(s) per socket: 4
Socket(s): 1
Stepping: 12
CPU max MHz: 4900.0000
CPU min MHz: 400.0000
BogoMIPS: 4599.93
Flags: fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mc
a cmov pat pse36 clflush dts acpi mmx fxsr sse sse2 ss
ht tm pbe syscall nx pdpe1gb rdtscp lm constant_tsc art
arch_perfmon pebs bts rep_good nopl xtopology nonstop_
tsc cpuid aperfmperf pni pclmulqdq dtes64 monitor ds_cp
l vmx est tm2 ssse3 sdbg fma cx16 xtpr pdcm pcid sse4_1
sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsav
e avx f16c rdrand lahf_lm abm 3dnowprefetch cpuid_fault
epb invpcid_single ssbd ibrs ibpb stibp ibrs_enhanced
tpr_shadow vnmi flexpriority ept vpid ept_ad fsgsbase t
sc_adjust sgx bmi1 avx2 smep bmi2 erms invpcid mpx rdse
ed adx smap clflushopt intel_pt xsaveopt xsavec xgetbv1
xsaves dtherm ida arat pln pts hwp hwp_notify hwp_act_
window hwp_epp md_clear flush_l1d arch_capabilities
Virtualization features:
Virtualization: VT-x
Caches (sum of all):
L1d: 128 KiB (4 instances)
L1i: 128 KiB (4 instances)
L2: 1 MiB (4 instances)
L3: 8 MiB (1 instance)
NUMA:
NUMA node(s): 1
NUMA node0 CPU(s): 0-7
Vulnerabilities:
Itlb multihit: KVM: Mitigation: VMX disabled
L1tf: Not affected
Mds: Not affected
Meltdown: Not affected
Mmio stale data: Mitigation; Clear CPU buffers; SMT vulnerable
Retbleed: Mitigation; Enhanced IBRS
Spec store bypass: Mitigation; Speculative Store Bypass disabled via prctl
and seccomp
Spectre v1: Mitigation; usercopy/swapgs barriers and __user pointer
sanitization
Spectre v2: Mitigation; Enhanced IBRS, IBPB conditional, RSB fillin
g, PBRSB-eIBRS SW sequence
Srbds: Mitigation; Microcode
Tsx async abort: Not affectedFrom the output of lscpu, one can see the L1d and L1i are the L1 caches for data and instructions, both having a size of 128 KB. The L2 and L3 caches are larger, they have size 1 MB and 8 MB respectively. Depending on the different energy strategy and the payload, the CPU clock rate can vary between 0.4 GHz and 4.9 GHz. The flags tell the information about the instruction sets, among which the avx2 instruction set is for the single instruction multiple data (SIMD) parallelism. It uses a 256 wide register to pack 4 double precision floating point numbers or 8 single precision floating point numbers, and perform multiply and add operation on them in a single CPU clock cycle.
A CPU may have multiple cores, and its theoretical upper bound of computing power can be measured by the number of floating point operations your computing device and perform in one second, namely, in floating point operations per second (FLOPS). For the above CPU, the computing power can be estimated with
Double precision computing power of a CPU = 4.9 (CPU clock speed)
* 2 (due to the fused multiply-add (`fma`) instruction)
* 4 (avx instruction set has a 256 with register, it can
crunch 4 vectorized double precision floating point
operations at one CPU cycle)
* 4 (number of cores)
* sometimes extra factor
= ? GFLOPSAn easy way to check the single/double precision FLOPS is using the matrix multiplication. Try the following code in a Julia REPL
julia> using LinearAlgebra
julia> LinearAlgebra.versioninfo()
BLAS: libblastrampoline.so (f2c_capable)
--> /home/leo/.julia/juliaup/julia-1.9.0-beta2+0.x64.linux.gnu/bin/../lib/julia/libopenblas64_.so (ILP64)
Threading:
Threads.threadpoolsize() = 1
Threads.maxthreadid() = 1
LinearAlgebra.BLAS.get_num_threads() = 1
Relevant environment variables:
OPENBLAS_NUM_THREADS = 1
julia> n = 1000
1000
julia> A, B, C = randn(Float64, n, n), randn(Float64, n, n), zeros(Float64, n, n);
julia> BLAS.set_num_threads(1)
julia> @benchmark mul!($C, $A, $B)
BenchmarkTools.Trial: 108 samples with 1 evaluation.
Range (min … max): 44.629 ms … 55.949 ms ┊ GC (min … max): 0.00% … 0.00%
Time (median): 46.178 ms ┊ GC (median): 0.00%
Time (mean ± σ): 46.571 ms ± 1.634 ms ┊ GC (mean ± σ): 0.00% ± 0.00%
▁▁█▅▁ ▁
▃▃▆▃▆██████▇█▇▇▅▅▃▁▃▄▁▁▃▃▁▄▁▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃▁▁▁▁▁▃ ▃
44.6 ms Histogram: frequency by time 54.1 ms <
Memory estimate: 0 bytes, allocs estimate: 0.
julia> BLAS.set_num_threads(4)
julia> @benchmark mul!($C, $A, $B)
BenchmarkTools.Trial: 299 samples with 1 evaluation.
Range (min … max): 15.252 ms … 26.505 ms ┊ GC (min … max): 0.00% … 0.00%
Time (median): 16.303 ms ┊ GC (median): 0.00%
Time (mean ± σ): 16.716 ms ± 1.831 ms ┊ GC (mean ± σ): 0.00% ± 0.00%It can be shown that the computing power of a single thread is at least . The computing time of a carefully implemented matrix multiplication function is dominated by the multiplication operations and the same amount of addition operations. Dividing floating point operations in total by the amount of time in the the unit of seconds is the peak FLOPS. Here we have used the minimum computing time because the system does not always allocate time slices to the program we want to benchmark, using the minimum time gives us the best approximate to the time we want to measure.
For the parallel execution, although we have 4 CPU cores, the 4-thread computation does not give us a 4 time speed up. This may have different causes, the cores may share caches, the operating system may not allocate all resources to this specific computing task.
In addition, since we are using intel CPU, MKL is slightly faster than the default OpenBLAS. If we repeat the above numerical experiment, we will get the following timing information, which measures the peak performance of a CPU more acurately.
julia> using MKL
julia> LinearAlgebra.versioninfo()
BLAS: libblastrampoline.so (f2c_capable)
--> /home/leo/.julia/artifacts/347e4bf25d69805922225ce6bf819ef0b8715426/lib/libmkl_rt.so (ILP64)
--> /home/leo/.julia/artifacts/347e4bf25d69805922225ce6bf819ef0b8715426/lib/libmkl_rt.so (LP64)
Threading:
Threads.threadpoolsize() = 1
Threads.maxthreadid() = 1
LinearAlgebra.BLAS.get_num_threads() = 4
Relevant environment variables:
OPENBLAS_NUM_THREADS = 1
julia> BLAS.set_num_threads(1)
julia> @benchmark mul!($C, $A, $B)
BenchmarkTools.Trial: 113 samples with 1 evaluation.
Range (min … max): 42.150 ms … 50.687 ms ┊ GC (min … max): 0.00% … 0.00%
Time (median): 44.179 ms ┊ GC (median): 0.00%
Time (mean ± σ): 44.434 ms ± 1.435 ms ┊ GC (mean ± σ): 0.00% ± 0.00%
▅▅▂▂▂▅▂▂▅ ▂▃ █
▄▄▁▇▇▄▇████████████▅█▇▄█▄▁▄▇▁▁▅▁▁▁▁▄▄▁▁▄▁▄▁▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▄ ▄
42.1 ms Histogram: frequency by time 50.4 ms <
Memory estimate: 0 bytes, allocs estimate: 0.
julia> BLAS.set_num_threads(4)
julia> @benchmark mul!($C, $A, $B)
BenchmarkTools.Trial: 281 samples with 1 evaluation.
Range (min … max): 14.882 ms … 26.696 ms ┊ GC (min … max): 0.00% … 0.00%
Time (median): 15.791 ms ┊ GC (median): 0.00%
Time (mean ± σ): 17.775 ms ± 3.766 ms ┊ GC (mean ± σ): 0.00% ± 0.00%
▃██▄
▄▇█████▄▃▃▂▁▁▁▃▃▂▂▂▁▂▁▃▂▁▁▂▁▁▁▁▁▁▂▁▁▁▁▁▁▁▁▁▁▁▂▁▁▁▁▂▂▃▄▆▆▅▃▃ ▃
14.9 ms Histogram: frequency by time 25.4 ms <
Memory estimate: 0 bytes, allocs estimate: 0.$ lsmem
RANGE SIZE STATE REMOVABLE BLOCK
0x0000000000000000-0x000000007fffffff 2G online yes 0-15
0x0000000088000000-0x000000008fffffff 128M online yes 17
0x0000000100000000-0x0000000a6fffffff 37.8G online yes 32-333
Memory block size: 128M
Total online memory: 39.9G
Total offline memory: 0BThe computing power of a GPU
You may check your GPU information with the following command,
$ nvidia-smi
Tue Feb 14 20:55:02 2023
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 510.108.03 Driver Version: 510.108.03 CUDA Version: 11.6 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 NVIDIA GeForce ... Off | 00000000:01:00.0 On | N/A |
| 30% 28C P8 7W / 75W | 815MiB / 4096MiB | 4% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+CUDA peak FLOPS is much easier to estimate, which is
Double precision computing power of a GPU = the GPU frequency
* the number of CUDA cores
* 2 (the `fma` support)One can verify the result with the official data sheet of a CUDA GPU or benchmark the CUDA performance with julia.
julia> using BenchmarkTools, CUDA
julia> using LinearAlgebra: mul!
julia> A, B = CUDA.randn(1000, 1000), CUDA.randn(1000, 1000);
julia> C = CUDA.zeros(1000, 1000);
julia> @benchmark CUDA.@sync mul!($C, $A, $B)
BenchmarkTools.Trial: 4206 samples with 1 evaluation.
Range (min … max): 814.601 μs … 13.147 ms ┊ GC (min … max): 0.00% … 0.00%
Time (median): 1.182 ms ┊ GC (median): 0.00%
Time (mean ± σ): 1.172 ms ± 264.659 μs ┊ GC (mean ± σ): 0.00% ± 0.00%
█▃ ▁▁ ▁▁
▂▂▁▂▂▂▂▃▃▃▄▆▄▅▅▅▆▆██▅▆▄▅▄▄▄▅▅▄▆▆▆▆▆██▇▆▅▆▅▇▇▇▆▇███▆▆▅▄▃▃▅▄▃▃▂ ▄
815 μs Histogram: frequency by time 1.45 ms <
Memory estimate: 416 bytes, allocs estimate: 24.